Precalculus Law of Sines Trigonometric Form Questions
Precalculus Law of Sines Trigonometric Form Questions
1.
Solve the triangle.
A = 46°, a = 31, b = 27 (5 points)
B = 38.8°, C = 115.2°, c ≈ 34.3
B = 38.8°, C = 95.2°, c ≈ 25.7
B = 38.8°, C = 95.2°, c ≈ 42.9
Cannot be solved
2.
State whether the given measurements determine zero, one, or two triangles.
A = 36°, a = 3, b = 9 (5 points)
Zero
Two
One
3.
Two triangles can be formed with the given information. Use the Law of Sines to solve the triangles.
B = 40°, b = 25, c = 26 (5 points)
A = 98°, C = 42°, a = 16.2; A = 2°, C = 138°, a = 16.2
A = 98°, C = 42°, a = 38.5; A = 2°, C = 138°, a = 1.4
A = 92°, C = 48°, a = 38.9; A = 88°, C = 132°, a = 38.9
A = 92°, C = 48°, a = 16.1; A = 88°, C = 132°, a = 16.1
4.
The given measurements may or may not determine a triangle. If not, then state that no triangle is formed. If a triangle is formed, then use the Law of Sines to solve the triangle, if it is possible, or state that the Law of Sines cannot be used.
B = 137°, c = 6, b = 11 (5 points)
The triangle cannot be solved with the Law of Sines.
C = 21.2°, A = 21.8°, a ≈ 5.8
No triangle is formed.
C = 21.8°, A = 21.2°, a ≈ 5.8
5.
Solve the triangle.
A = 52°, b = 10, c = 7 (5 points)
a ≈ 12, C ≈ 47.9, B ≈ 80.1
a ≈ 7.9, C ≈ 43.9, B ≈ 84.1
No triangles possible
a ≈ 12, C ≈ 43.9, B ≈ 84.1
6.
Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary.
A = 50°, b = 31 ft, c = 18 ft (5 points)
427.45 ft2
179.34 ft2
213.73 ft2
558 ft2
7.
Determine whether a triangle can be formed with the given side lengths. If so, use Heron’s formula to find the area of the triangle. (5 points)
a = 240
b = 121
c = 302
8.
A building has a ramp to its front doors to accommodate the handicapped. If the distance from the building to the end of the ramp is 13 feet and the height from the ground to the front doors is 5 feet, how long is the ramp? (Round to the nearest tenth.) (5 points)
12.0 ft
13.9 ft
4.2 ft
7.1 ft
9.
Given that P = (-4, 11) and Q = (-5, 8), find the component form and magnitude of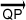 
. (5 points)
<1, 3>,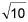 
<-9, 3>,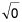 
<1, 3>, 10
<-1, -3>,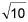
10.
Let u = <-6, 3>, v = <1, 9>. Find u – v. (5 points)
<-15, 2>
<-9,-8>
<-5, 12>
<-7, -6>
11.
Let u = <-6, 1>, v = <-5, 2>. Find -4u + 2v. (5 points)
<34, -8>
<14, 0>
<14, 3>
<44, -12>
12.
Find a ⋅ b.
a = 6i – 6j, b = 4i + 2j (5 points)
12
-36
<24, -12>
<10, -4>
13.
Find the angle between the given vectors to the nearest tenth of a degree.
u = <6, 4>, v = <7, 5> (5 points)
0.9°
1.8°
-9.1°
11.8°
14.
Determine whether the vectors u and v are parallel, orthogonal, or neither.
u = <8, 4>, v = <10, 7> (5 points)
Orthogonal
Neither
Parallel
15.
Evaluate the expression.
r = <5, 9, -4>, v = <3, 3, -8>, w = <9, -6, -1>
v ⋅ w (5 points)
<-15, -27, -32>
0
17
<27, -18, 8>
16.
Express the complex number in trigonometric form.
-4i (5 points)
4(cos 180° + i sin 180°)
4(cos 270° + i sin 270°)
4(cos 90° + i sin 90°)
4(cos 0° + i sin 0°)
17.
Express the complex number in trigonometric form.
-2 + 2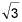 
i (5 points)
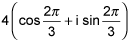
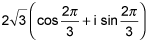
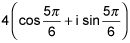
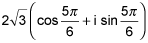
18.
Write the complex number in the form a + bi.
6(cos 330° + i sin 330°) (5 points)
-3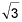 
– 3i
-3 + 3i
3 + 3i
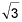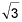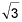3 – 3i
19.
Two forces with magnitudes of 150 and 100 pounds act on an object at angles of 30° and 120°, respectively. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and in your final answer. (5 points)
20.
Find the fourth roots of 16(cos 200° + i sin 200°). (5 points)
